Python深度学习之PyTorch基础教程

前言

PyTorch是一个基于Torch的Python开源机器学习(深度学习)框架，由Facebook的人工智能研究院开发，不仅能够实现强大的GPU加速，还支持动态神经网络，使得研究人员和开发人员能够轻松构建和训练复杂的深度学习模型。与TensorFlow等其他框架相比，Pytorch的主要优势在于其简单易用的接口、高效的性能和强大的生态系统。PyTorch的主要特点和功能：

• 基本概念：PyTorch的基本概念包括张量(Tensor)、自动求导(Autograd)和动态计算图(Dynamic Computation Graph)。张量是PyTorch最基本的数据类型，类似于多维数组，用于存储和处理大规模的数值数据，并支持各种数学运算和操作。自动求导是PyTorch的一个重要特性，它能自动计算张量的梯度，有助于深度学习模型的训练。动态计算图则使得PyTorch的计算过程可以灵活地进行构建和修改，有助于开发复杂的神经网络模型。
• 基本使用方法：PyTorch提供了丰富的API和工具，使得用户可以方便地创建和操作张量，进行基本的数学运算，以及构建和训练神经网络模型。例如，用户可以轻松地创建一个矩阵，进行加法操作，改变矩阵的维度，以及与NumPy进行协同操作等。
• 软件特色：PyTorch由多个库组成，包括Tensor库、自动分化库、神经网络库、多处理库和实用函数库等。这些库提供了丰富的功能和工具，使得PyTorch既可以作为Numpy的替代品，也可以作为深度学习研究平台，提供最佳的灵活性和速度。
• 生态系统组件：torchvision一个用于计算机视觉任务的库，包含常见数据集、预训练模型和工具；torchtext一个用于文本处理任务的库，支持文本清洗、分词等功能；torch.nn一个用于构建神经网络的模块，提供了各种层、损失函数和优化器；torch.distributed一个用于分布式训练的库，可以轻松实现多机多卡训练。
• 学习资源：PyTorch官方文档提供了详细的教程和API文档，适合初学者入门和深入学习。此外，PyTorch中文网、GitHub上的开源项目以及博客、论坛和在线社区等也提供了丰富的教程、解答和讨论，有助于用户更好地学习和使用PyTorch。
• 应用场景：PyTorch的应用场景非常广泛，包括图像识别、自然语言处理、计算机视觉等领域。例如，在图像识别领域，PyTorch可以用于训练图像分类器；在自然语言处理领域，PyTorch可以用于训练文本分类器；在计算机视觉领域，PyTorch可以用于实现计算机视觉推理系统等。

总的来说，PyTorch是一个功能强大、灵活易用的深度学习平台，适用于各种人工智能研究和应用场景。PyTorch是一个基于Python的科学计算包，主要定位两类人群：

• NumPy的替代品，可以利用GPU的性能进行计算；

• 深度学习研究平台拥有足够的灵活性和速度。

PyTorch基础

Numpy基础

在机器学习和深度学习中，图像、声音、文本等输入数据最终都要转换为数组或矩阵。如何有效地进行数组和矩阵的运算？这就需要充分利用Numpy。Numpy是数据科学的通用语言，而且与PyTorch关系非常密切，它是科学计算、深度学习的基石。尤其对PyTorch而言，其重要性更加明显。PyTorch中的Tensor与Numpy非常相似，它们之间可以非常方便地进行转换，掌握Numpy是学好PyTorch的重要基础。

Numpy(Numerical Python)提供了两种基本的对象：ndarray(N-dimensional Array Object)和ufunc(Universal Function Object)。ndarray是存储单一数据类型的多维数组，而ufunc则是能够对数组进行处理的函数。

Numpy数组

（1）从已有数据中创建数组

通过直接对Python的基础数据类型(如列表、元组等)进行转换来生成ndarray：

import numpy as np
# 将列表转换成ndarray
list1 = [3.5, 2.5, 0, 1, 2]
nd1 = np.array(list1)
print(nd1)
print(type(nd1))
# 嵌套列表可以转换成多维ndarray
list2 = [[3.5, 2.5, 0, 1, 2], [1, 2, 3, 4, 5]]
nd2 = np.array(list2)
print(nd2)
print(type(nd2))
# 将元组转换成ndarray
list3 = (0, 1, 2, 3, 4, 5, 6)
nd3 = np.array(list3)
print(nd3)
print(type(nd3))

# 输出结果
[3.5 2.5 0.  1.  2. ]
<class 'numpy.ndarray'>
[[3.5 2.5 0.  1.  2. ]
 [1.  2.  3.  4.  5. ]]
<class 'numpy.ndarray'>
[0 1 2 3 4 5 6]
<class 'numpy.ndarray'>

（2）利用random模块生成数组

在深度学习中，我们需要对一些参数进行初始化，为了更有效地训练模型，提高模型的性能，有些初始化还需要满足一定的条件，如满足正态分布或均匀分布等。np.random模块常用函数：

函数	描述
np.random.random	生成0到1之间的随机数
np.random.uniform	生成均匀分布的随机数
np.random.randn	生成标准正态的随机数
np.random.randint	生成随机的整数
np.random.normal	生成正态分布
np.random.shuffle	随机打乱顺序
np.random.seed	设置随机数种子
np.random.random_sample	生成随机的浮点数
…	…

import numpy as np
nd = np.random.random([3, 3])
print(nd)
print(nd.shape)
np.random.shuffle(nd)
print(nd)

# 输出结果
[[0.96651734 0.71544924 0.70717421]
 [0.92522016 0.99484174 0.00550428]
 [0.36218919 0.11263693 0.1816698 ]]
(3, 3)
[[0.92522016 0.99484174 0.00550428]
 [0.96651734 0.71544924 0.70717421]
 [0.36218919 0.11263693 0.1816698 ]]

（3）创建特定形状的多维数组

参数初始化时，有时需要生成一些特殊矩阵，如全是0或1的数组或矩阵。

函数	描述
np.zeros((m,n))	创建m×n的元素全为0的数组
np.ones((m,n))	创建m×n的元素全为1的数组
np.empty((m,n))	创建m×n的空数组，空数据中的值并不为0，而是未初始化的垃圾值
np.zeros_like(ndarr)	以ndarr相同维度创建元素全为0数组
np.ones_like(ndarr)	以ndarr相同维度创建元素全为1数组
np.empty_like(ndarr)	以ndarr相同维度创建空数组
np.eye(m)	该函数用于创建一个m×m的矩阵，对角线为1，其余为0
np.full((m,n), value)	创建m×n的元素全为value的数组，value为指定值
…	…

（4）利用arange、linspace函数生成数组

# numpy模块中的arange、linspace函数
# start与stop用来指定范围，step用来设定步长。在生成一个ndarray时，start默认为0，步长step可为小数。Python有个内置函数range，其功能与此类似。
np.arange([start,] stop[,step,], dtype=None)
# linspace可以根据输入的指定数据范围以及等份数量，自动生成一个线性等分向量，其中endpoint（包含终点）默认为True，等分数量num默认为50。如果将retstep设置为True，则会返回一个带步长的ndarray。
np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)

获取元素

import numpy as np
nd = np.random.random([10])
print(nd)
# 获取指定位置的数据，获取第4个元素
print(nd[3])
# 截取一段数据
print(nd[3:6])
# 截取固定间隔数据
print(nd[1:6:2])
# 倒序取数
print(nd[::-2])
# 截取一个多维数组的一个区域内数据
nd1 = np.arange(25).reshape([5, 5])
print(nd1)
print(nd1[1:3, 1:3])
# 截取一个多维数组中，数值在一个值域之内的数据
print(nd1[(nd1 > 3) & (nd1 < 10)])
# 截取多维数组中，指定的行,如读取第2,3行
print(nd1[[1, 2]])  # 或nd12[1:3,:]
# 截取多维数组中，指定的列,如读取第2,3列
print(nd1[:, 1:3])

获取数组中的部分元素除了通过指定索引标签来实现外，还可以通过使用一些函数来实现，如通过random.choice函数从指定的样本中随机抽取数据。

Numpy的算术运算

在机器学习和深度学习中，涉及大量的数组或矩阵运算，我们将重点介绍两种常用的运算。

• 一种是对应元素相乘，又称为逐元乘法(Element-Wise Product)，运算符为np.multiply()或*。

• 一种是点积或内积元素，运算符为np.dot()。

（1）对应元素相乘

对应元素相乘(Element-Wise Product)是两个矩阵中对应元素乘积。np.multiply函数用于数组或矩阵对应元素相乘，输出与相乘数组或矩阵的大小一致，其格式如下：

# 格式
# x1、x2之间的对应元素相乘遵守广播规则
numpy.multiply(x1, x2, /, out=None, *, where=True, casting='same_kind', order='K', dtype=None, subok=True[, signature, extobj])

# 示例
import numpy as np
A = np.array([[1, 2], [-1, 4]])
B = np.array([[2, 0], [3, 4]])
print(A*B)
print(np.multiply(A, B))
# Numpy数组不仅可以和数组进行对应元素相乘，还可以和单一数值（或称为标量）进行运算。运算时，Numpy数组中的每个元素都和标量进行运算，其间会用到广播机制
print(A*2.0)
print(A/2.0)

# 输出结果
[[ 2  0]
 [-3 16]]
[[ 2  0]
 [-3 16]]
[[ 2.  4.]
 [-2.  8.]]
[[ 0.5  1. ]
 [-0.5  2. ]]

由此，推而广之，数组通过一些激活函数后，输出与输入形状一致。

import numpy as np
X = np.random.rand(2, 3)
def softmoid(x):
    return 1 / (1 + np.exp(-x))
def relu(x):
    return np.maximum(0, x)
def softmax(x):
    return np.exp(x) / np.sum(np.exp(x))
print("输入参数X的形状：", X.shape)
print("激活函数softmoid输出形状：", softmoid(X).shape)
print("激活函数relu输出形状：", relu(X).shape)
print("激活函数softmax输出形状：", softmax(X).shape)

# 输出结果
输入参数X的形状： (2, 3)
激活函数softmoid输出形状： (2, 3)
激活函数relu输出形状： (2, 3)
激活函数softmax输出形状： (2, 3)

（2）点积运算

# 格式
numpy.dot(a, b, out=None)

# 示例
# 矩阵X1和矩阵X2进行点积运算，其中X1和X2对应维度（即X1的第2个维度与X2的第1个维度）的元素个数必须保持一致。此外，矩阵X3的形状是由矩阵X1的行数与矩阵X2的列数构成的。
import numpy as np
X1 = np.array([[1, 2], [3, 4]])
X2 = np.array([[5, 6, 7], [8, 9, 10]])
X3 = np.dot(X1, X2)
print(X3)

# 输出结果
[[21 24 27]
 [47 54 61]]

数组变形

在机器学习及深度学习的任务中，通常需要将处理好的数据以模型能接收的格式输入给模型，然后由模型通过一系列的运算，最终返回一个处理结果。然而，由于不同模型所接收的输入格式不一样，往往需要先对其进行一系列的变形和运算，从而将数据处理成符合模型要求的格式。在矩阵或者数组的运算中，经常会遇到需要把多个向量或矩阵按某轴方向合并，或展平（如在卷积或循环神经网络中，在全连接层之前，需要把矩阵展平）的情况。

（1）更改数组的形状

修改指定数组的形状是Numpy中最常见的操作之一，常见函数：

函数	描述
arr.reshape	重新将向量arr维度进行改变，不修改向量本身
arr.resize	重新将向量arr维度进行改变，修改向量本身
arr.T	对向量arr进行转置
arr.ravel	对向量arr进行展平，即将多维数组变成1维数组，不会产生原数组的副本
arr.flatten	对向量arr进行展平，即将多维数组变成1维数组，返回原数组的副本
arr.squeeze	只能对维数为1的维度降维。对多维数组使用时不会报错，但是不会产生任何影响
arr.transpose	对高维矩阵进行轴对换

import numpy as np

arr = np.arange(10)
print(arr)
print("*" * 20)
# (1)reshape改变向量的维度（不修改向量本身）：
# 将向量 arr 维度变换为2行5列
print(arr.reshape(2, 5))
# 指定维度时可以只指定行数或列数, 其他用-1代替
print(arr.reshape(5, -1))
print(arr.reshape(-1, 5))
print("*" * 20)
# (2)resize改变向量的维度（修改向量本身）
# 将向量 arr 维度变换为2行5列
arr.resize(2, 5)
print(arr)
print("*" * 20)
# (3)T向量转置
# 将向量arr进行转置为5行2列
print(arr.T)
print("*" * 20)
# (4)ravel向量展平
# 按照列优先，展平
print("按照列优先，展平")
print(arr.ravel('F'))
# 按照行优先，展平
print("按照行优先，展平")
print(arr.ravel())
print("*" * 20)
# (5)flatten把矩阵转换为向量，这种需求经常出现在卷积网络与全连接层之间。
print(arr.flatten())
print("*" * 20)
# (6)squeeze这是一个主要用来降维的函数，把矩阵中含1的维度去掉。
arr1 = np.arange(3).reshape(3, 1)
print(arr1.shape)  # (3,1)
print(arr1.squeeze().shape)  # (3,)
arr2 = np.arange(6).reshape(3, 1, 2, 1)
print(arr2.shape)  # (3, 1, 2, 1)
print(arr2.squeeze().shape)  # (3, 2)
print("*" * 20)
# (7)transpose对高维矩阵进行轴对换，在深度学习中经常使用，比如把图片中表示颜色顺序的RGB改为GBR。
arr3 = np.arange(24).reshape(2, 3, 4)
print(arr3.shape)  # (2, 3, 4)
print(arr3.transpose(1, 2, 0).shape)  # (3, 4, 2)

# 输出结果
[0 1 2 3 4 5 6 7 8 9]
********************
[[0 1 2 3 4]
 [5 6 7 8 9]]
[[0 1]
 [2 3]
 [4 5]
 [6 7]
 [8 9]]
[[0 1 2 3 4]
 [5 6 7 8 9]]
********************
[[0 1 2 3 4]
 [5 6 7 8 9]]
********************
[[0 5]
 [1 6]
 [2 7]
 [3 8]
 [4 9]]
********************
按照列优先，展平
[0 5 1 6 2 7 3 8 4 9]
按照行优先，展平
[0 1 2 3 4 5 6 7 8 9]
********************
[0 1 2 3 4 5 6 7 8 9]
********************
(3, 1)
(3,)
(3, 1, 2, 1)
(3, 2)
********************
(2, 3, 4)
(3, 4, 2)

（2）合并数组

合并数组也是最常见的操作之一，常见的用于数组或向量合并的方法。

函数	描述
np.append	合并一维或多维数组，内存占用大
np.concatenate	沿指定轴连接数组或矩阵，没有内存问题
np.stack	沿指定轴堆叠数组或矩阵，沿着新的轴加入一系列数组
np.hstack	按水平方向（列顺序）堆叠数组构成一个新的数组，堆叠的数组需要具有相同的维度
np.vstack	按垂直方向（行顺序）堆叠数组构成一个新的数组，堆叠的数组需要具有相同的维度
np.dstack	沿深度方向将数组进行堆叠。将相同尺寸的数组沿着第三个维度（深度方向）进行水平叠加，返回一个新的数组。
np.hsplit	将一个数组水平（列）分割成多个子数组
np.vsplit	将一个数组垂直（行）分割成多个子数组

• append、concatenate以及stack都有一个axis参数，用于控制数组的合并方式是按行还是按列。

• 对于append和concatenate，待合并的数组必须有相同的行数或列数（满足一个即可）。

• stack、hstack、dstack，要求待合并的数组必须具有相同的形状(shape)。

• numpy.hsplit(arr, indices_or_sections)和numpy.vsplit(arr, indices_or_sections)：①arr是要拆分的多维数组或矩阵[ndarray]；②indices_or_sections : [int or 1-D array] 如果indices_or_sections是一个整数N，数组将沿轴线被分成N个相等的数组。如果indices_or_sections是一个排序的整数的一维数组，这些整数表示该数组沿轴线的分割位置。

import numpy as np

# (1)append
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
c = np.append(a, b)
print(c)
print("*" * 20)
a1 = np.arange(4).reshape(2, 2)
b1 = np.arange(4).reshape(2, 2)
# 按行合并
c1 = np.append(a1, b1, axis=0)
print('按行合并后的结果')
print(c1)
print('合并后数据维度', c1.shape)
# 按列合并
d2 = np.append(a1, b1, axis=1)
print('按列合并后的结果')
print(d2)
print('合并后数据维度', d2.shape)
print("*" * 20)
# (2)concatenate沿指定轴连接数组或矩阵
a3 = np.array([[1, 2], [3, 4]])
b3 = np.array([[5, 6]])
c3 = np.concatenate((a3, b3), axis=0)
print(c3)
d3 = np.concatenate((a3, b3.T), axis=1)
print(d3)
print("*" * 20)
# (3)stack沿指定轴堆叠数组或矩阵,axis=0/1/2
a4 = np.array([[1, 2], [3, 4]])
b4 = np.array([[5, 6], [7, 8]])
print(np.stack((a4, b4), axis=1))
print("*" * 20)
# (3)vstack和hstack
a5 = np.array([[1, 2, 3]])
b5 = np.array([[4, 5, 6]])
print(np.vstack((a5, b5)))
print(np.hstack((a5, b5)))
print("*" * 20)
# (4)dstack
a6 = np.array([[1, 2, 3], [4, 5, 6]])
b6 = np.array([[7, 8, 9], [10, 11, 12]])
print(np.dstack((a6, b6)))

# 输出结果
[1 2 3 4 5 6]
********************
按行合并后的结果
[[0 1]
 [2 3]
 [0 1]
 [2 3]]
合并后数据维度 (4, 2)
按列合并后的结果
[[0 1 0 1]
 [2 3 2 3]]
合并后数据维度 (2, 4)
********************
[[1 2]
 [3 4]
 [5 6]]
[[1 2 5]
 [3 4 6]]
********************
[[[1 2]
  [5 6]]

 [[3 4]
  [7 8]]]
********************
[[1 2 3]
 [4 5 6]]
[[1 2 3 4 5 6]]
********************
[[[ 1  7]
  [ 2  8]
  [ 3  9]]

 [[ 4 10]
  [ 5 11]
  [ 6 12]]]

批量处理

在深度学习中，由于源数据都比较大，通常需要用到批处理。如利用批量来计算梯度的随机梯度法(SGD)就是一个典型应用。深度学习的计算一般比较复杂，并且数据量一般比较大，如果一次处理整个数据，较大概率会出现资源瓶颈。为了更有效地计算，一般将整个数据集分批次处理。与处理整个数据集相反的另一个极端是每次只处理一条记录，这种方法也不科学，一次处理一条记录无法充分发挥GPU、Numpy的平行处理优势。因此，在实际使用中往往采用批量处理(Mini-Batch)的方法。如何把大数据拆分成多个批次呢？可采用如下步骤：

1. 数据集
2. 随机打乱数据：shuffle()
3. 定义批大小：batch_size
4. 批处理数据集

通用函数

ufunc是universal function的缩写，它是一种能对数组的每个元素进行操作的函数。许多ufunc函数都是用C语言级别实现的，因此它们的计算速度非常快。此外，它们比math模块中的函数更灵活。math模块的输入一般是标量，但Numpy中的函数可以是向量或矩阵，而利用向量或矩阵可以避免使用循环语句，这点在机器学习、深度学习中非常重要。Numpy中的几个常用通用函数：

函数	描述
sqrt	计算序列化数据的平方根
sin、cos	三角函数
abs	计算序列化数据的绝对值
dot	矩阵运算
log、log10、1og2	对数运算
exp	指数运算
cumsum、cumproduct	累计求和、求积
sum	对一个序列化数据进行求和
mean	计算均值
median	计算中位数
std	计算标准差
var	计算方差
corrcoef	计算相关系数

广播机制

Numpy的Universal functions中要求输入的数组shape是一致的，当数组的shape不相等时，则会使用广播机制。不过，调整数组使得shape一样，需要满足一定的规则，否则将出错。这些规则可归纳为以下4条。

• 让所有输入数组都向其中shape最长的数组看齐，不足的部分则通过在前面加1补齐；
• 输出数组的shape是输入数组shape的各个轴上的最大值；
• 如果输入数组的某个轴和输出数组的对应轴的长度相同或者某个轴的长度为1时，这个数组能被用来计算，否则出错；
• 当输入数组的某个轴的长度为1时，沿着此轴运算时都用(或复制)此轴上的第一组值。

例子：A+B，其中A为4×1矩阵，B为一维向量（3,）。要相加，需要做如下处理：

1. 根据规则1，B需要向看齐，把B变为（1, 3）
2. 根据规则2，输出的结果为各个轴上的最大值，即输出结果应该为（4, 3）矩阵，那么A如何由（4, 1）变为（4, 3）矩阵？B又如何由（1, 3）变为（4, 3）矩阵？
3. 根据规则4，用此轴上的第一组值(要主要区分是哪个轴)，进行复制(但在实际处理中不是真正复制，否则太耗内存，而是采用其他对象如ogrid对象，进行网格处理)即可。

import numpy as np
A = np.arange(0, 40,10).reshape(4, 1)
B = np.arange(0, 3)
print("A矩阵的形状:{},B矩阵的形状:{}".format(A.shape,B.shape))
C = A+B
print("C矩阵的形状:{}".format(C.shape))
print(C)

# 输出结果
A矩阵的形状:(4, 1),B矩阵的形状:(3,)
C矩阵的形状:(4, 3)
[[ 0  1  2]
 [10 11 12]
 [20 21 22]
 [30 31 32]]

PyTorch基础

PyTorch是建立在Torch库之上的Python包，旨在加速深度学习应用。它提供一种类似Numpy的抽象方法来表征张量(或多维数组)，可以利用GPU加速训练。PyTorch采用了动态计算图(Dynamic Computational Graph)结构，且基于tape的Autograd系统的深度神经网络。很多框架，比如TensorFlow(TensorFlow2.0也加入动态网络的支持)、Caffe、CNTK、Theano等采用静态计算图。PyTorch通过一种称为反向模式自动微分的技术，可以零延迟或零成本地任意改变你的网络的行为。Torch是PyTorch中的一个重要包，它包含了多维张量的数据结构以及基于其上的多种数学操作。PyTorch由4个主要的包组成：

• torch：类似Numpy的通用数组库，将张量类型转换为torch.cuda.TensorFloat，并在GPU上计算。
• torch.autograd：用于构建计算图形并自动获取梯度的包。
• torch.nn：具有共享层和损失函数的神经网络库。
• torch.optim：具有通用优化算法(如SGD、Adam等)的优化包。

Tensor概述

PyTorch的Tensor，它可以是零维(又称为标量或一个数)、一维、二维及多维的数组。Tensor自称为神经网络界的Numpy，它与Numpy相似，二者可以共享内存，且之间的转换非常方便高效。它们最大的区别就是Numpy会把ndarray放在CPU中进行加速运算，而由Torch产生的Tensor会放在GPU中进行加速运算(假设当前环境有GPU)。对Tensor的操作很多，从接口的角度来划分，可以分为两类：

• torch.function，如torch.sum、torch.add等；

• tensor.function，如tensor.view、tensor.add等。

这些操作对大部分Tensor都是等价的，如torch.add(x,y)与x.add(y)等价。在实际使用时，可以根据个人爱好选择。如果从修改方式的角度来划分，可以分为以下两类：

• 不修改自身数据，如x.add(y)，x的数据不变，返回一个新的Tensor。

• 修改自身数据，如x.add_(y)（运行符带下划线后缀），运算结果存在x中，x被修改。

创建Tensor

创建Tensor的方法有很多，可以从列表或ndarray等类型进行构建，也可根据指定的形状构建。常见的创建Tensor的方法：

函数	描述
Tensor()	直接从参数构造一个张量，支持List、Numpy数组
eye(row, column)	创建指定行数、列数的二维单位Tensor
linspace(start, end, steps)	从start到end，均匀切分成steps份
logspace(start, end, steps)	从10^start，到10^end，均匀切分成steps份
rand/randn(*size)	生成[0, 1)均匀分布/标准正态分布数据
ones(*size)	返回指定shape的张量，元素初始为1
zeros(*size)	返回指定shape的张量，元素初始为0
ones_like(T)	返回与T的shape相同的张量，且元素初始为1
zeros_like(T)	返回与T的shape相同的张量，且元素初始为0
arange(start, end, step)	在区间[start, end)上以间隔step生成一个序列张量
from_Numpy(ndarray)	从ndarray创建一个Tensor

import torch

# 根据list数据生成Tensor
a = torch.Tensor([1, 2, 3, 4, 5, 6])
print(a)
print("*"*20)
# 根据指定形状生成Tensor，随机初始化
b = torch.Tensor(2, 3)
print(b)
print("*"*20)
# 根据给定的Tensor的形状
c = torch.Tensor([[1, 2, 3], [4, 5, 6]])
print(c)
# 查看Tensor的形状
print(c.size())
# shape与size()等价方式
print(c.shape)
print("*"*20)
# 根据已有形状创建Tensor，随机初始化
d = torch.Tensor(c.size())
print(d)
# 生成一个单位矩阵
torch.eye(2, 2)
# 自动生成全是0的矩阵
torch.zeros(2, 3)
# 根据规则生成数据
torch.linspace(1, 10, 4)
# 生成满足均匀分布随机数
torch.rand(2, 3)
# 生成满足标准分布随机数
torch.randn(2, 3)
# 返回所给数据形状相同，值全为0的张量
torch.zeros_like(torch.rand(2, 3))

# 输出结果
tensor([1., 2., 3., 4., 5., 6.])
********************
tensor([[7.2564e+24, 1.7418e-42, 0.0000e+00],
        [0.0000e+00, 0.0000e+00, 0.0000e+00]])
********************
tensor([[1., 2., 3.],
        [4., 5., 6.]])
torch.Size([2, 3])
torch.Size([2, 3])
********************
tensor([[7.2567e+24, 1.7418e-42, 0.0000e+00],
        [0.0000e+00, 0.0000e+00, 0.0000e+00]])

注意torch.Tensor与torch.tensor的几点区别：

1）torch.Tensor是torch.empty和torch.tensor之间的一种混合，但当传入数据时，torch.Tensor使用全局默认dtype(FloatTensor)，而torch.tensor是从数据中推断数据类型。

2）torch.tensor(1)返回一个固定值1，而torch.Tensor(1)返回一个大小为1的张量，它是随机初始化的值。

import torch
t1 = torch.Tensor(3)
t2 = torch.Tensor(1)
t3 = torch.tensor(1)
print("t1的值{},t1的数据类型{}".format(t1, t1.type()))
print("t2的值{},t2的数据类型{}".format(t2, t2.type()))
print("t3的值{},t3的数据类型{}".format(t3, t3.type()))

# 输出结果1
t1的值tensor([7.0406e+13, 1.1561e-42, 0.0000e+00]),t1的数据类型torch.FloatTensor
t2的值tensor([0.]),t2的数据类型torch.FloatTensor
t3的值1,t3的数据类型torch.LongTensor

# 输出结果2
t1的值tensor([0., 0., 0.]),t1的数据类型torch.FloatTensor
t2的值tensor([3.4713e-18]),t2的数据类型torch.FloatTensor
t3的值1,t3的数据类型torch.LongTensor

修改Tensor形状

在处理数据、构建网络层等过程中，需要了解Tensor的形状、修改Tensor的形状。与修改Numpy的形状类似，修改Tenor的形状也有很多类似函数：

函数	描述
size()	返回张量的shape属性值，与属性shape(0.4版新增)等价
numel(input)	计算Tensor的元素个数
view(*shape)	修改Tensor的shape，与reshape(0.4版新增)类似，但view返回的对象与源Tensor共享内存，修改一个，另一个同时修改。reshape将生成新的Tensor，而且不要求源Tensor是连续的。view(-1)展平数组
resize	类似于view，但在size超出时会重新分配内存空间
item	若Tensor为单(一个)元素，则返回Python的标量
unsqueeze	扩展维度，在插入维度的索引位置增加维度"1",这里的"1"仅仅起到扩展维度的作用
squeeze	降低维度，在压缩维度的索引位置减少维度"1"，即将输入张量形状指定位置中的"1"去除并返回

import torch

# 生成一个形状为2x3的矩阵
x = torch.randn(2, 3)
# 查看矩阵的形状
print(x.size())
# 查看x的维度
print(x.dim())
print("*"*20)
# 把x变为3x2的矩阵
print(x.view(3, 2))
# 把x展平为1维向量
y = x.view(-1)
print(y.shape)
print("*"*20)
# 添加一个维度
z = torch.unsqueeze(y, 0)
# 查看z的形状
print(z.size())
# 计算Z的元素个数
print(z.numel())
print("*"*20)
# item()的用法
a = torch.tensor([1])
print(a.item())
b = torch.tensor([2, 3, 4, 5])
print(b.tolist())

# 输出结果
torch.Size([2, 3])
2
********************
tensor([[-0.4888,  1.4943],
        [-1.6593, -0.6757],
        [-1.9228, -1.0863]])
torch.Size([6])
********************
torch.Size([1, 6])
6
********************
1
[2, 3, 4, 5]

torch.view与torch.reshpae的异同

1）reshape()可由torch.reshape()，也可由torch.Tensor.reshape()调用。但view()只可由torch.Tensor.view()来调用。

2）对于一个将要被view的Tensor，新的size必须与原来的size与stride兼容。否则，在view之前必须调用contiguous()方法。

3）返回与input数据量相同，但形状不同的Tensor。若满足view的条件，则不会copy，若不满足，则会copy。

4）如果只是重塑张量，请使用torch.reshape。如果还关注内存使用情况并希望确保两个张量共享相同的数据，请使用torch.view。

索引操作

Tensor的索引操作与Numpy类似，一般情况下索引结果与源数据共享内存。从Tensor获取元素除了可以通过索引，也可以借助一些函数，常用的选择函数如下：

函数	描述
index_select(input, dim, index)	在指定维度上选择行和列
nonzero(input)	获取非0元素的下标
masked_select(input, mask)	使用二元值进行选择
gather(input, dim, index)	在指定维度上选择数据，输出形状与index(类型是LongTensor)一致
scatter__(dim, index, src)	为gather的反操作，根据指定索引补充数据

import torch

# 设置一个随机种子
torch.manual_seed(100)
# 生成一个形状为2x3的矩阵
x = torch.randn(2, 3)
print(x)
# 根据索引获取第1行，所有数据
print(x[0, :])
# 获取最后一列数据
print(x[:, -1])
# 生成是否大于0的Byter张量
mask = x > 0
print(mask)
# 获取大于0的值
print(torch.masked_select(x, mask))
# 获取非0下标,即行，列索引
print(torch.nonzero(mask))
print("*"*20)
# 获取指定索引对应的值
index1 = torch.LongTensor([[0, 1, 1]])
print(torch.gather(x, 0, index1))
index2 = torch.LongTensor([[0, 1, 1], [1, 1, 1]])
a = torch.gather(x, 1, index2)
print(a)
# 把a的值返回到一个2x3的0矩阵中
z = torch.zeros(2, 3)
z.scatter_(1, index2, a)
print(z)

# 输出结果
tensor([[ 0.3607, -0.2859, -0.3938],
        [ 0.2429, -1.3833, -2.3134]])
tensor([ 0.3607, -0.2859, -0.3938])
tensor([-0.3938, -2.3134])
tensor([[ True, False, False],
        [ True, False, False]])
tensor([0.3607, 0.2429])
tensor([[0, 0],
        [1, 0]])
********************
tensor([[ 0.3607, -1.3833, -2.3134]])
tensor([[ 0.3607, -0.2859, -0.2859],
        [-1.3833, -1.3833, -1.3833]])
tensor([[ 0.3607, -0.2859,  0.0000],
        [ 0.0000, -1.3833,  0.0000]])

广播机制

PyTorch也支持广播机制：

import torch
import numpy as np

A = np.arange(0, 40, 10).reshape(4, 1)
B = np.arange(0, 3)
# 把ndarray转换为Tensor
A1 = torch.from_numpy(A)  # 形状为4x1
B1 = torch.from_numpy(B)  # 形状为3
# Tensor自动实现广播
C = A1 + B1
print(C)
# 我们可以根据广播机制，手工进行配置
# 根据规则1，B1需要向A1看齐，把B变为（1,3）
B2 = B1.unsqueeze(0)  # B2的形状为1x3
# 使用expand函数重复数组，分别的4x3的矩阵
A2 = A1.expand(4, 3)
B3 = B2.expand(4, 3)
# 然后进行相加,C1与C结果一致
C1 = A2 + B3
print(C1)

# 输出结果
tensor([[ 0,  1,  2],
        [10, 11, 12],
        [20, 21, 22],
        [30, 31, 32]], dtype=torch.int32)
tensor([[ 0,  1,  2],
        [10, 11, 12],
        [20, 21, 22],
        [30, 31, 32]], dtype=torch.int32)

逐元素操作

与Numpy一样，Tensor也有逐元素操作(Element-Wise)，且操作内容相似，但使用函数可能不尽相同。大部分数学运算都属于逐元素操作，其输入与输出的形状相同。这些操作均会创建新的Tensor，如果需要就地操作，可以使用这些方法的下划线版本，例如abs_。常见的函数如下：

函数	描述
abs/add	绝对值/加法
addcdiv(t, v, t1, t2)	t1与t2的按元素除后，乘v加t；（可能弹出"UserWarning"）
addcmul(t, v, t1, t2)	t1与t2的按元素乘后，乘v加t；（可能弹出"UserWarning"）
ceil/floor	向上取整/向下取整
clamp(t, min, max)	将张量元素限制在指定区间
exp/log/pow	指数/对数/幂
mul(或*)/neg	逐元素乘法/取反
sigmoid/tanh/softmax	激活函数
sign/sqrt	取输入张量元素的符号/开根号

import torch

t = torch.randn(1, 3)
t1 = torch.randn(3, 1)
t2 = torch.randn(1, 3)
print(t)
print(t1)
print(t2)
print("*"*20)
print(torch.addcdiv(t, 0.1, t1, t2))
print("*"*20)
# 计算sigmoid
print(torch.sigmoid(t))
print("*"*20)
# 将t限制在[0,1]之间
print(torch.clamp(t, 0, 1))
print("*"*20)
# t+2进行就地运算
t.add_(2)
print(t)

# 输出结果
tensor([[ 2.4080,  0.6269, -0.0157]])
tensor([[-0.3307],
        [-0.6533],
        [ 0.7257]])
tensor([[ 0.6907, -0.8531, -0.8397]])
********************
tensor([[ 2.3601,  0.6656,  0.0237],
        [ 2.3134,  0.7035,  0.0621],
        [ 2.5131,  0.5418, -0.1021]])
********************
tensor([[0.9174, 0.6518, 0.4961]])
********************
tensor([[1.0000, 0.6269, 0.0000]])
********************
tensor([[4.4080, 2.6269, 1.9843]])

归并操作

归并操作，就是对输入进行归并或合计等操作，这类操作的输入输出形状一般并不相同，而且往往是输入大于输出形状。归并操作可以对整个Tensor，也可以沿着某个维度进行归并。常见的函数如下：

函数	描述
cumprod(t, axis)	在指定维度对t进行累积
cumsum	在指定维度对t进行累加
dist(a, b, p=2)	返回a, b之间的p阶范数
mean/median	均值/中位数
std/var	标准差/方差
norm(t, p=2)	返回t的p阶范数
prod(t)/sum(t)	返回t所有元素的积/和

归并操作一般涉及一个dim参数，指定沿哪个维进行归并。另一个参数是keepdim，说明输出结果中是否保留维度1，缺省情况是False，即不保留。

import torch

# 生成一个含6个数的向量
a = torch.linspace(0, 10, 6)
print(a)
print("*"*20)
# 使用view方法，把a变为2x3矩阵
a = a.view((2, 3))
print(a)
print("*"*20)
# 沿y轴方向累加，即dim=0
b = a.sum(dim=0)  # b的形状为[3]
print(b)
print(b.shape)
print("*"*20)
# 沿y轴方向累加，即dim=0,并保留含1的维度
b = a.sum(dim=0, keepdim=True)  # b的形状为[1,3]
print(b)
print(b.shape)

# 输出结果
tensor([ 0.,  2.,  4.,  6.,  8., 10.])
********************
tensor([[ 0.,  2.,  4.],
        [ 6.,  8., 10.]])
********************
tensor([ 6., 10., 14.])
torch.Size([3])
********************
tensor([[ 6., 10., 14.]])
torch.Size([1, 3])

比较操作

比较操作一般是进行逐元素比较，有些是按指定方向比较。常见的函数如下：

函数	描述
eq	比较Tensor是否相等(逐元素比较)，支持broadcast
equal	比较Tensor是否有相同的shape与值(张量比较)
ge/le/gt/lt	大于等于/小于等于/大于/小于
max/min(t, axis)	返回最值，若指定axis，则额外返回下标
topk(t, k, axis)	在指定的axis维上取最高的K个值

import torch

x = torch.linspace(0, 10, 6).view(2, 3)
print(x)
print("*"*20)
# 求所有元素的最大值
print(torch.max(x))  # 结果为10
print("*"*20)
# 求y轴方向的最大值
print(torch.max(x, dim=0))  # 结果为[6, 8, 10]
print("*"*20)
# 求最大的2个元素
# 结果为[6, 8, 10],对应索引为tensor([[1, 1, 1]
print(torch.topk(x, 1, dim=0))

# 输出结果
tensor([[ 0.,  2.,  4.],
        [ 6.,  8., 10.]])
********************
tensor(10.)
********************
torch.return_types.max(
values=tensor([ 6.,  8., 10.]),
indices=tensor([1, 1, 1]))
********************
torch.return_types.topk(
values=tensor([[ 6.,  8., 10.]]),
indices=tensor([[1, 1, 1]]))

矩阵操作

机器学习和深度学习中存在大量的矩阵运算，常用的算法有两种：一种是逐元素乘法，另外一种是点积乘法。常见的函数如下：

函数	描述
dot(t1, t2)	计算张量（1D）的内积或点积
mm(mat1, mat2)/bmm(batch1, batch2)	计算矩阵乘法/含batch的3D矩阵乘法
mv(t1, v1)	计算矩阵与向量乘法
t	转置
svd(t)	计算t的SVD分解

• Torch的dot与Numpy的dot有点不同，Torch中的dot是对两个为1D张量进行点积运算，Numpy中的dot无此限制。

• mm是对2D的矩阵进行点积，bmm对含batch的3D进行点积运算。

• 转置运算会导致存储空间不连续，需要调用contiguous方法转为连续。

import torch

a = torch.tensor([2, 3])
b = torch.tensor([3, 4])
print(torch.dot(a, b))    # 运行结果为18
print("*"*20)
x = torch.randint(10, (2, 3))
y = torch.randint(6, (3, 4))
print(torch.mm(x, y))
print("*"*20)
x = torch.randint(10, (2, 2, 3))
y = torch.randint(6, (2, 3, 4))
print(torch.bmm(x, y))

# 输出结果
tensor(18)
********************
tensor([[47, 20, 20, 39],
        [55, 22, 35, 27]])
********************
tensor([[[ 57,  45,  40,  60],
         [ 47,  10,  24,  43]],

        [[ 54, 106,  36, 104],
         [ 34,  42,   4,  50]]])

PyTorch与Numpy比较

PyTorch与Numpy有很多类似的地方，并且有很多相同的操作函数名称，或虽然函数名称不同但含义相同；当然也有一些虽然函数名称相同，但含义不尽相同。

操作类别	Numpy	PyTorch
数据类型	np.ndarray	torch.Tensor
	np.float32	torch.float32; torch.float
	np.float64	torch.float64; torch.double
	np.int64	torch.int64; torch.long
已有数据构建	np.array([1.3, 1.4], dtype=np.float32)	torch.tensor([1.3, 1.4], dtype=torch.float32)
	x.copy()	x.clone()
	np.concatenate	torch.cat
线性代数	np.dot	torch.mm
属性	x.ndim	x.dim()
	x.size	x.nelement()
形状操作	x.reshape	x.reshape; x.view
	x.flatten	x.view(-1)
类型转换	np.floor(x)	torch.floor(x); x.floor()
比较	np.less	x.lt
	np.less_equal/np.greater	x.le/x.gt
	np.greater_equal/np.equal/np.not_equal	x.ge/x.eq/x.ne
随机种子	np.random.seed	torch.manual.seed

Tensor与Autograd

神经网络一个重要内容就是进行参数学习，而参数学习离不开求导，那么PyTorch是如何进行求导的呢？

现在大部分深度学习架构都有自动求导的功能，PyTorch也不例外，torch.autograd包就是用来自动求导的。Autograd包为张量上所有的操作提供了自动求导功能，而torch.Tensor和torch.Function为Autograd的两个核心类，它们相互连接并生成一个有向非循环图。为实现对Tensor自动求导，需考虑如下事项：

• 创建叶子节点(Leaf Node)的Tensor，使用requires_grad参数指定是否记录对其的操作，以便之后利用backward()方法进行梯度求解。requires_grad参数的缺省值为False，如果要对其求导需设置为True，然后与之有依赖关系的节点会自动变为True。

• 可利用requires_grad_()方法修改Tensor的requires_grad属性。可以调用.detach()或with torch.no_grad()，将不再计算张量的梯度，跟踪张量的历史记录。这点在评估模型、测试模型阶段中常常用到。

• 通过运算创建的Tensor（即非叶子节点），会自动被赋予grad_fn属性，该属性表示梯度函数。叶子节点的grad_fn为None。

• 最后得到的Tensor执行backward()函数，此时自动计算各变量的梯度，并将累加结果保存到grad属性中。计算完成后，非叶子节点的梯度自动释放。

• backward()函数接收参数，该参数应和调用backward()函数的Tensor的维度相同，或者是可broadcast的维度。如果求导的Tensor为标量（即一个数字），则backward中的参数可省略。

• 反向传播的中间缓存会被清空，如果需进行多次反向传播，需指定backward中的参数retain_graph=True。多次反向传播时，梯度是累加的。

• 非叶子节点的梯度backward调用后即被清空。

• 可以通过用torch.no_grad()包裹代码块的形式来阻止autograd去跟踪那些标记为.requesgrad=True的张量的历史记录。这步在测试阶段经常使用。

标量反向传播：当目标张量为标量时，可以调用backward()方法且无须传入参数。目标张量一般都是标量，如我们经常使用的损失值Loss，一般都是一个标量。

非标量反向传播：PyTorch规定，不让张量(Tensor)对张量求导，只允许标量对张量求导。因此，如果目标张量对一个非标量调用backward()，则需要传入gradient参数，该参数也是张量，而且需要与调用backward()的张量形状相同。传入这个参数就是为了把张量对张量的求导转换为标量对张量的求导。

# 标量反向传播
import torch

# 定义输入张量x
x = torch.Tensor([2])
# 初始化权重参数W,偏移量b、并设置require_grad属性为True，为自动求导
w = torch.randn(1, requires_grad=True)
b = torch.randn(1, requires_grad=True)
# 实现前向传播
y = torch.mul(w, x)  # 等价于w*x
z = torch.add(y, b)  # 等价于y+b
# 查看x,w，b页子节点的requite_grad属性
# x,w,b的require_grad属性分别为：False,True,True
print("x, w, b的require_grad属性分别为：{},{},{}".format(x.requires_grad, w.requires_grad, b.requires_grad))
# 查看非叶子节点的requres_grad属性
# 因与w，b有依赖关系，故y，z的requires_grad属性也是：True,True
print("y, z的requires_grad属性分别为：{},{}".format(y.requires_grad, z.requires_grad))
# 查看各节点是否为叶子节点
# x，w，b，y，z的是否为叶子节点：True,True,True,False,False
print("x, w, b, y, z的是否为叶子节点：{},{},{},{},{}".format(x.is_leaf, w.is_leaf, b.is_leaf, y.is_leaf, z.is_leaf))
# 查看叶子节点的grad_fn属性
# 因x，w，b为用户创建的，为通过其他张量计算得到，故x，w，b的grad_fn属性：None,None,None
print("x, w, b的grad_fn属性：{},{},{}".format(x.grad_fn, w.grad_fn, b.grad_fn))
# 查看非叶子节点的grad_fn属性
print("y, z的是否为叶子节点：{},{}".format(y.grad_fn, z.grad_fn))

# 输出结果
x, w, b的require_grad属性分别为：False,True,True
y, z的requires_grad属性分别为：True,True
x, w, b, y, z的是否为叶子节点：True,True,True,False,False
x, w, b的grad_fn属性：None,None,None
y, z的是否为叶子节点：<MulBackward0 object at 0x000001DCB56E94C0>,<AddBackward0 object at 0x000001DCB56E92B0>

PyTorch神经网络工具箱

PyTorch的神经网络工具箱，可以极大简化我们构建模型的任务，设计一个神经网络就像搭积木一样。神经网络核心组件主要包括：

• 层：神经网络的基本结构，将输入张量转换为输出张量。

• 模型：层构成的网络。

• 损失函数：参数学习的目标函数，通过最小化损失函数来学习各种参数。

• 优化器：如何使损失函数最小，这就涉及优化器。

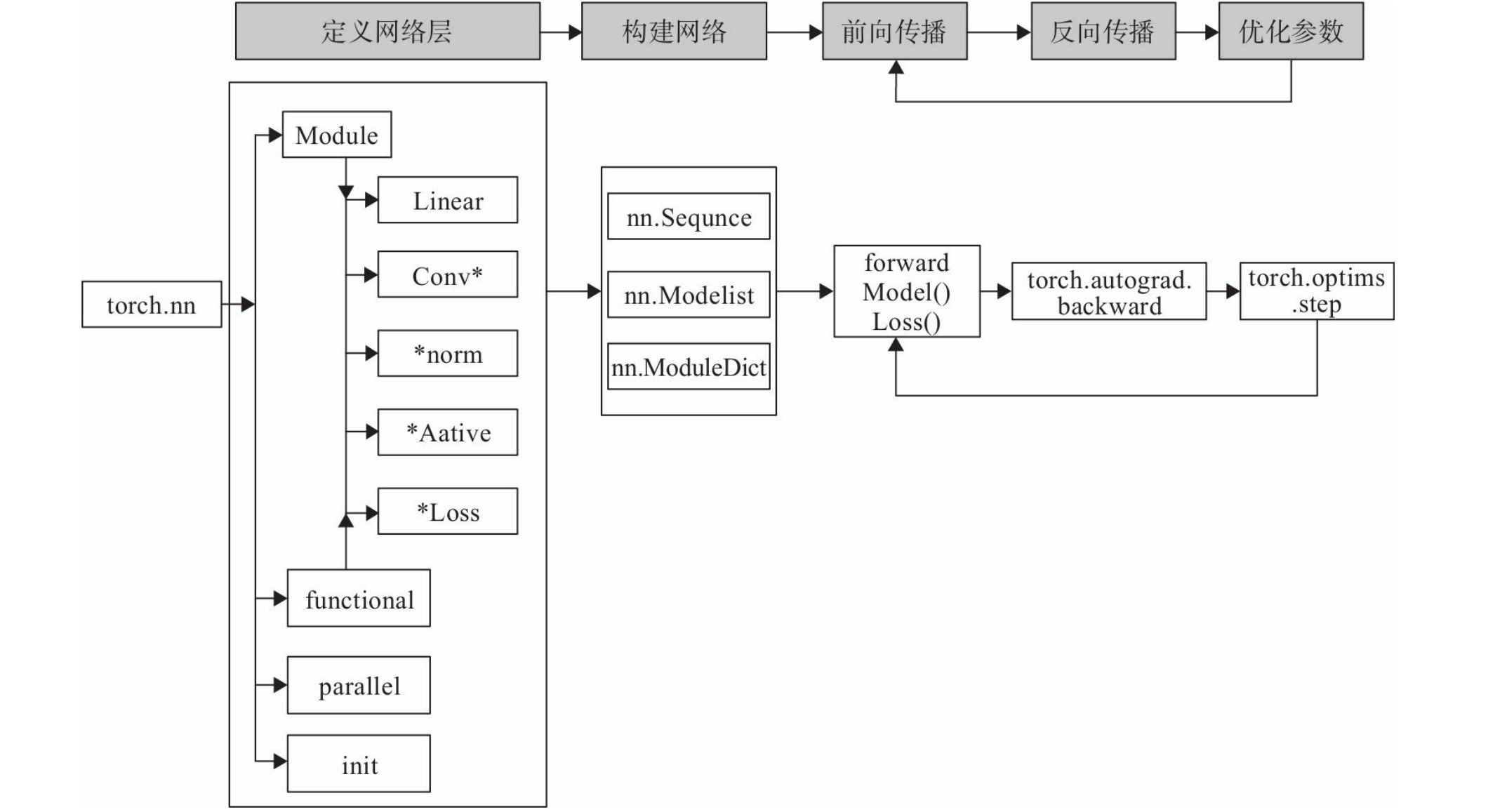
多个层链接在一起构成一个模型或网络，输入数据通过这个模型转换为预测值，然后损失函数把预测值与真实值进行比较，得到损失值（损失值可以是距离、概率值等），该损失值用于衡量预测值与目标结果的匹配或相似程度，优化器利用损失值更新权重参数，从而使损失值越来越小。这是一个循环过程，当损失值达到一个阀值或循环次数到达指定次数，循环结束。PyTorch构建神经网络使用的主要工具（或类）及相互关系如下图所示：

构建网络层可以基于Module类或函数(nn.functional)。nn中的大多数层(Layer)在functional中都有与之对应的函数。nn.functional中函数与nn.Module中的Layer的主要区别是后者继承Module类，会自动提取可学习的参数。而nn.functional更像是纯函数。两者功能相同，且性能也没有很大区别，那么如何选择呢？像卷积层、全连接层、Dropout层等因含有可学习参数，一般使用nn.Module，而激活函数、池化层不含可学习参数，可以使用nn.functional中对应的函数。

• 构建网络：使用sequential构建网络，Sequential()函数的功能是将网络的层组合到一起。
• 前向传播：①forward()函数的任务是把输入层、网络层、输出层链接起来，实现信息的前向传导，该函数的参数一般为输入数据，返回值为输出数据。②在forward函数中，有些层来自nn.Module，也可以使用nn.functional定义。来自nn.Module的需要实例化，而使用nn.functional定义的可以直接使用。
• 反向传播：①手工实现反向传播，比较费时；②PyTorch提供了自动反向传播的功能，直接让损失函数调用backward()即可。
• 训练模型：①训练模型时需要使模型处于训练模式，即调用model.train()，会把所有的module设置为训练模式。如果是测试或验证阶段，需要使模型处于验证阶段，即调用model.eval()，会把所有的training属性设置为False。②缺省情况下梯度是累加的，需要调用optimizer.zero_grad()把梯度初始化或清零。③训练过程中，正向传播生成网络的输出，计算输出和实际值之间的损失值，调用loss.backward()自动生成梯度，然后使用optimizer.step()执行优化器，把梯度传播回每个网络。④如果希望用GPU训练，需要把模型、训练数据、测试数据发送到GPU上，即调用.to(device)。如果需要使用多GPU进行处理，可使模型或相关数据引用nn.DataParallel。

nn.Module

nn.Module是nn的一个核心数据结构，它可以是神经网络的某个层(Layer)，也可以是包含多层的神经网络。在实际使用中，最常见的做法是继承nn.Module，生成自己的网络/层。nn中已实现了绝大多数层，包括全连接层、损失层、激活层、卷积层、循环层等，这些层都是nn.Module的子类，能够自动检测到自己的Parameter，并将其作为学习参数，且针对GPU运行进行了cuDNN优化。

nn.functional

nn中的层，一类是继承了nn.Module，其命名一般为nn.Xxx(第一个是大写)，如nn.Linear、nn.Conv2d、nn.CrossEntropyLoss等。另一类是nn.functional中的函数，其名称一般为nn.funtional.xxx，如nn.funtional.linear、nn.funtional.conv2d、nn.funtional.cross_entropy等。从功能来说两者相当，基于nn.Moudle能实现的层，使用nn.funtional也可实现，反之亦然，而且性能方面两者也没有太大差异。不过在具体使用时，两者还是有区别，主要区别如下：

• nn.Xxx继承于nn.Module，nn.Xxx需要先实例化并传入参数，然后以函数调用的方式调用实例化的对象并传入输入数据。它能够很好地与nn.Sequential结合使用，而nn.functional.xxx无法与nn.Sequential结合使用。

• nn.Xxx不需要自己定义和管理weight、bias参数；而nn.functional.xxx需要自己定义weight、bias参数，每次调用的时候都需要手动传入weight、bias等参数，不利于代码复用。

• Dropout操作在训练和测试阶段是有区别的，使用nn.Xxx方式定义Dropout，在调用model.eval()之后，自动实现状态的转换，而使用nn.functional.xxx却无此功能。

总的来说，两种功能都是相同的，但PyTorch官方推荐：具有学习参数的(例如Conv2d、Linear、Batch_norm等)采用nn.Xxx方式。没有学习参数的(例如maxpool、loss func、activation func等)根据个人选择使用nn.Xxx或者nn.functional.xxx方式。

优化器

（1）优化器一般步骤

PyTorch常用的优化方法都封装在torch.optim里面，其设计很灵活，可以扩展为自定义的优化方法。所有的优化方法都是继承了基类optim.Optimizer，并实现了自己的优化步骤。最常用的优化算法就是梯度下降法及其各种变种，这类优化算法通过使用参数的梯度值更新参数。使用优化器的一般步骤为：

• 建立优化器实例：导入optim模块，实例化SGD（以随机梯度下降法为例）优化器。

• 向前传播：把输入数据传入神经网络Net实例化对象model中，自动执行forward函数，得到out输出值（out = model(img)），然后用out与标记label计算损失值loss。loss = criterion(out, label)

• 清空梯度：缺省情况梯度是累加的，在梯度反向传播前，先需把梯度清零。optimizer.zero_grad()

• 反向传播：基于损失值，把梯度进行反向传播。loss.backward()

• 更新参数：基于当前梯度（存储在参数的.grad属性中）更新参数。optimizer.step()

其中向前传播、清空梯度、反向传播、更新参数是在训练模型的for循环中。

动态修改学习率参数：可以通过修改参数optimizer.params_groups或新建optimizer。新建optimizer比较简单，optimizer十分轻量级，所以开销很小。但是新的优化器会初始化动量等状态信息，这对于使用动量的优化器（momentum参数的sgd）可能会造成收敛中的震荡。

optimizer.param_groups：长度1的list；

optimizer.param_groups[0]：长度为6的字典，包括权重参数、lr、momentum等参数。

（2）优化器种类

优化器的方法主要可以分为两大类，一大类方法是SGD及其改进（加Momentum），另外一大类是逐参数适应学习率方法，包括AdaGrad、RMSProp、Adam等。参考链接①、参考链接②、参考链接③

• SGD(Stochastic Gradient Descent, 随机梯度下降)

• SGD+Momentum动量法

• NAG(Nesterov Accelerated Gradient)

• Adagrad自适应学习率优化算法

• RMSProp自适应学习率优化算法

• Adam自适应学习率优化算法，本质上是将动量(Momentum)和RMSprop两种思想结合到一种算法中

PyTorch数据处理工具箱

utils.data和Torchvision

数据下载和预处理是机器学习、深度学习实际项目中耗时又重要的任务，尤其是数据预处理，关系到数据质量和模型性能，要占据项目的大部分时间。PyTorch为此提供了专门的数据下载、数据处理包，使用这些包可极大地提高开发效率及数据质量。PyTorch涉及数据处理（数据装载、数据预处理、数据增强等）的主要工具包及相互关系如下图所示。

torch.utils.data工具包，它包括以下4个类。

• Dataset：是一个抽象类，其他数据集需要继承这个类，并且覆写其中的两个方法(getitem、len)。

• DataLoader：定义一个新的迭代器，实现批量(batch)读取，打乱数据(shuffle)并提供并行加速等功能。

• random_split：把数据集随机拆分为给定长度的非重叠的新数据集。

• *sampler：多种采样函数。

Torchvision是PyTorch的一个视觉处理工具包，独立于PyTorch。它包括4个类，主要功能如下(参考博客①)：

• datasets：提供常用的数据集加载，设计上都是继承自torch.utils.data.Dataset，主要包括MMIST、CIFAR10/100、Fashion-MNIST、ImageNet、STL10和COCO等。

• models：提供深度学习中各种经典的网络结构以及训练好的模型（如果选择pretrained=True），包括AlexNet、VGG系列、ResNet系列、Inception系列等。

• transforms：常用的数据预处理操作，主要包括对Tensor及PIL Image对象的操作。

• utils：含两个函数，一个是make_grid，它能将多张图片拼接在一个网格中；另一个是save_img，它能将Tensor保存成图片。

tensorboardX可视化工具

Tensorboard是Google TensorFlow的可视化工具，它可以记录训练数据、评估数据、网络结构、图像等，并且可以在web上展示，对于观察神经网络训练的过程非常有帮助。PyTorch可以采用tensorboard_logger、visdom等可视化工具，但这些方法比较复杂或不够友好。为解决该问题，人们推出了可用于PyTorch可视化的新的更强大的工具——tensorboardX。tensorboardX功能很强大，支持scalar、image、figure、histogram、audio、text、graph、onnx_graph、embedding、pr_curve and videosummaries等可视化方式。参考博客①、参考博客②

（1）导入tensorboardX，实例化SummaryWriter类，指明记录日志路径等信息

from tensorboardX import SummaryWriter
# 实例化SummaryWriter，并指明日志存放路径。在当前目录没有logs目录将自动创建。
writer = SummaryWriter(log_dir='logs')
# 调用实例
writer.add_xxx()
# 关闭writer
writer.close()

（2）调用相应的API接口

writer.add_xxx(tag-name, object, iteration-number)
# 即add_xxx(标签，记录的对象，迭代次数)

（3）启动tensorboard服务

tensorboard --logdir=logs --port 6006
# 如果是Windows环境，要注意路径解析，如
# tensorboard --logdir=r'D:\myboard\test\logs' --port 6006

（4）web展示

http://服务器IP或名称:6006 # 如果是本机，服务器名称可以使用localhost

多谢！多谢！
笔者不才，请多交流！！！

欢迎大家关注预览我的博客Blog：HeartLoveLife
能力有限，敬请谅解！！